2013年NOIP提高组初赛真题

一、单项选择题（共 15 题，每题 1.5 分，共计 22.5 分；每题有且仅有一个正确选项）

1. 一个 32 位整型变量占用（）个字节。

A. 4
B. 8
C. 32
D. 128

2. 二进制数 11.01 在十进制下是（）。

A. 3.25
B. 4.125
C. 6.25
D. 11.125

3. 下面的故事与（）算法有着异曲同工之妙。 从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：‚从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：‘从前有座山，山里有座庙，庙里有个老和尚给小和尚讲故事....’‛

A. 枚举
B. 递归
C. 贪心
D. 分治

4. 1948 年，（）将热力学中的熵引入信息通信领域，标志着信息论研究的开端。

A. 冯•诺伊曼（John von Neumann）
B. 图灵（Alan Turing）
C. 欧拉（Leonhard Euler）
D. 克劳德•香农（Claude Shannon）

5. 已知一棵二叉树有 2013 个节点，则其中至多有（）个节点有 2 个子节点。

A. 1006
B. 1007
C. 1023
D. 1024

6. 在一个无向图中，如果任意两点之间都存在路径相连，则称其为连通图。右图是一个有 5 个顶点、8 条边的连通图。若要使它不再是连通图，至少要删去其中的（）条边。

A. 2
B. 3
C. 4
D. 5

7. 斐波那契数列的定义如下：F1 = 1, F2 = 1, Fn = Fn – 1 + Fn – 2 (n ≥ 3)。如果用下面的函数计算斐波那契数列的第 n 项，则其时间复杂度为（）。 funtion F(n : longint) : longint; begin if n <= 2 then F := 1 else F := F(n - 1) + F(n - 2); end;

A. O(1)
B. O(n)
C. O(n2)
D. O(Fn)

8. 二叉查找树具有如下性质：每个节点的值都大于其左子树上所有节点的值、小于其右子树上所有节点的值。那么，二叉查找树的（）是一个有序序列。

A. 先序遍历
B. 中序遍历
C. 后序遍历
D. 宽度优先遍历

9. 将（2, 6, 10, 17）分别存储到某个地址区间为 0~10 的哈希表中，如果哈希函数 h(x) = （），将不会产生冲突，其中 a mod b 表示 a 除以 b 的余数。

A. x mod 11
B. x^2 mod 11
C. 2x mod 11
D.
E. √
F. mod 11，其中
G. √
H. H.表示√ 下取整

10. IPv4 协议使用 32 位地址，随着其不断被分配，地址资源日趋枯竭。因此，它正逐渐被使用（）位地址的 IPv6 协议所取代。

A. 40
B. 48
C. 64
D. 128

11. 二分图是指能将顶点划分成两个部分，每一部分内的顶点间没有边相连的简单无向图。那么，12 个顶点的二分图至多有（）条边。

A. 18
B. 24
C. 36
D. 66

12. （）是一种通用的字符编码，它为世界上绝大部分语言设定了统一并且唯一的二进制编码，以满足跨语言、跨平台的文本交换。目前它已经收录了超过十万个不同字符。

A. ASCII
B. Unicode
C. GBK 2312
D. BIG5

13. 把 64 位非零浮点数强制转换成 32 位浮点数后，不可能（）。

A. 大于原数
B. 小于原数
C. 等于原数
D. 与原数符号相反

14. 对一个 n 个顶点、m 条边的带权有向简单图用 Dijkstra 算法计算单源最短路时，如果不 使用堆或其它优先队列进行优化，则其时间复杂度为（）。

A. O(mn + n3)
B. O(n2)
C. O((m + n) log n)
D. O((m + n2) log n)

15. T(n)表示某个算法输入规模为 n 时的运算次数。如果 T(1)为常数，且有递归式 T(n) = 2*T(n / 2) + 2n，那么 T(n) = （）。

A. Θ(n)
B. Θ(n log n)
C. Θ(n2)
D. Θ(n2 log n)

二、不定项选择题（共 5 题，每题 1.5 分，共计 7.5 分；每题有一个或多个正确选项，多选或少选均不得分）

16. 下列程序中，正确计算 1, 2, …, 100 这 100 个自然数之和 sum（初始值为 0）的是（）。

A. for i := 1 to 100 do sum := sum + i;
B. i := 1; while i > 100 do begin sum := sum + i; inc(i); end;
C. i := 1; repeat sum := sum + i; inc(i); until i > 100;
D. i := 1; repeat sum := sum + i; inc(i); until i <= 100;

17. （）的平均时间复杂度为 O(n log n)，其中 n 是待排序的元素个数。

A. 快速排序
B. 插入排序
C. 冒泡排序
D. 归并排序

18. 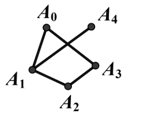以 A0 作为起点，对下面的无向图进行深度优先遍历时（遍历的顺序与顶点字母的下标无关），最后一个遍历到的顶点可能是（）。

A. A1
B. A2
C. A3
D. A4

19. （）属于 NP 类问题。

A. 存在一个 P 类问题
B. 任何一个 P 类问题
C. 任何一个不属于 P 类的问题
D. 任何一个在（输入规模的）指数时间内能够解决的问题

20. CCF NOIP 复赛考试结束后，因（）提出的申诉将不会被受理。

A. 源程序文件名大小写错误
B. 源程序保存在指定文件夹以外的位置
C. 输出文件的文件名错误
D. 只提交了可执行文件，未提交源程序

三、问题求解（共 2 题，每题 5 分，共计 10 分；每题全部答对得 5 分，没有部分分）

21. 某系统自称使用了一种防窃听的方式验证用户密码。密码是 n 个数 s1, s2, …, sn，均为 0 或 1。该系统每次随机生成 n 个数 a1, a2, …, an，均为 0 或 1，请用户回答(s1a1 + s2a2 + … + snan)除以 2 的余数。如果多次的回答总是正确，即认为掌握密码。该系统认为，即使问答的过程被泄露，也无助于破解密码——因为用户并没有直接发送密码。 然而，事与愿违。例如，当 n = 4 时，有人窃听了以下 5 次问答： 就破解出了密码 s1 =_________，s2 = _________，s3 =_________，s4 =_________。

22. 现有一只青蛙，初始时在 n 号荷叶上。当它某一时刻在 k 号荷叶上时，下一时刻将等概率地随机跳到 1, 2, …, k 号荷叶之一上，直至跳到 1 号荷叶为止。当 n = 2 时，平均一共跳 2 次；当 n = 3 时，平均一共跳 2.5 次。则当 n = 5 时，平均一共跳_________次。

四、阅读程序写结果（共 4 题，每题 8 分，共计 32 分）

23.

var 
n, i : integer; str : string; isPlalindrome : boolean;
begin readln(str);
n := Length(str);
isPlalindrome := true;
for i := 1 to (n div 2) do begin
if (str[i] <> str[n-i+1]) then
isPlalindrome := false;
end;
if (isPlalindrome) then writeln('Yes')
else
writeln('No');
end.
输入：abceecba
输出：____①_____

24.

var 
a, b, u, v, i, num : integer; 
begin
readln(a, b, u, v);
num := 0;
for i := a to b do begin
if (i mod u = 0) or (i mod v = 0) then inc(num); 
end;
writeln(num);
end.
输入：1 1000 10 15
输出：____①_____

25.

const SIZE = 100;
var
n, ans, i, j : integer;
height, num : array[1..SIZE] of integer;
begin read(n);
for i := 1 to n do begin
read(height[i]);
num[i] := 1;
for j := 1 to i-1 do begin
if ((height[j] < height[i]) and (num[j] >= num[i])) then
num[i] := num[j]+1;
end;
end;
ans := 0;
for i := 1 to n do begin
if (num[i] > ans) then
ans := num[i];
end;
writeln(ans);
end.
输入：
8
3 2 5 11 12 7 4 10
输出：____①_____

26.

const SIZE = 100;
var
n, m, p, count, ans, x, y, i, j : integer;
a : array[1..SIZE, 1..SIZE] of integer;
procedure colour(x, y : integer);
begin inc(count); a[x][y] := 1;
if (x > 1) and (a[x-1][y] = 0) then colour(x-1, y);
if (y > 1) and (a[x][y-1] = 0) then
colour(x, y-1);
if (x < n) and (a[x+1][y] = 0) then colour(x+1, y);
if (y < m) and (a[x][y+1] = 0) then
colour(x, y+1);
end;
begin
fillchar(a, sizeof(a), 0);
readln(n, m, p); for i := 1 to p do begin
read(x, y);
a[x][y] := 1;
end;
ans := 0;
for i := 1 to n do
for j := 1 to m do
if a[i][j] = 0 then begin
count := 0;
colour(i, j);
if (ans < count) then ans := count; 
end;
writeln(ans);
end.
输入：
6	5 9
1	4
2	3
2	4
3	2
4	1
4	3
4	5
5	4
6	4
输出：____①_____

五、完善程序（第 1 题 15 分，第 2 题 13 分，共计 28 分）

27. （序列重排）全局数组变量 a 定义如下： const int SIZE = 100; int a[SIZE], n; 它记录着一个长度为 n 的序列 a[1], a[2], …, a[n]。 现在需要一个函数，以整数 p (1 ≤ p ≤ n)为参数，实现如下功能：将序列 a 的前 p 个数与后 n – p 个数对调，且不改变这 p 个数（或 n – p 个数）之间的相对位置。例如，长度为 5 的序列 1, 2, 3, 4, 5，当 p = 2 时重排结果为 3, 4, 5, 1, 2。 有一种朴素的算法可以实现这一需求，其时间复杂度为 O(n)、空间复杂度为 O(n)：


procedure swap1(p : longint);
var
  i, j : longint;
  b : array[1..SIZE] of longint;
begin
  for i := 1 to p do
    b[ ____①_____ ] := a[i];	//（2 分）
  for i := p + 1 to n do 
    b[i - p] := a[i];
  for i := 1 to n do
    a[i] := b[i];
end;
我们也可以用时间换空间，使用时间复杂度为 O(n2)、空间复杂度为 O(1)的算法：
procedure swap2(p : longint);
var
  i, j, temp : longint;
begin
  for i := p + 1 to n do
  begin
    temp := a[i];
	for j := i downto ____②_____ do	//（2 分）
	  a[j] := a[j - 1];
	   ____③_____	:= temp;	//（2 分）
  end;
end;
事实上，还有一种更好的算法，时间复杂度为 O(n)、空间复杂度为 O(1)：
procedure swap3(p : longint);
var
  start1, end1, start2, end2, i, j, temp : longint;
begin
  start1 := 1;
  end1 := p;
  start2 := p + 1;
  end2 := n;
  while true do
  begin
    i := start1;
	j := start2;
	while (i <= end1) and (j <= end2) do 
	begin
	  temp := a[i];
	  a[i] := a[j];
	  a[j] := temp; 
	  inc(i); inc(j);
	end;
	if i <= end1 then
  	  start1 := i
	else if	____④_____	then	//（3 分）
	begin
	  start1 :=  ____⑤_____  ;                  //（3 分） 
	  end1 :=  ____⑥_____  ;                 //（3 分） start2 := j;
	end
	else
	  break;
   end;
end;

28. （两元序列）试求一个整数序列中，最长的仅包含两个不同整数的连续子序列。如有多个子序列并列最长，输出任意一个即可。例如，序列“1 1 2 3 2 3 2 3 3 1 1 1 3 1”中，有两段满足条件的最长子序列，长度均为 7，分别用下划线和上划线标出。


program two;
const SIZE = 100;
var
  n, i, j, cur1, cur2, count1, count2, ans_length, ans_start, ans_end : longint;
  //cur1, cur2  分别表示当前子序列中的两个不同整数
  //count1, count2 分别表示 cur1, cur2 在当前子序列中出现的次数
  a : array[1..SIZE] of longint;
begin
  readln(n);
  for i := 1 to n do read(a[i]);
  i := 1;
  j := 1;
  //i, j 分别表示当前子序列的首尾，并保证其中至多有两个不同整数
  while (j <= n) and (a[j] = a[i]) do
    inc(j);
  cur1 := a[i];
  cur2 := a[j];
  count1 :=	____①_____	;	//（3 分）
  count2 := 1;
  ans_length := j - i + 1;
  while j < n do
  begin
    inc(j);
	if a[j] = cur1 then
	  inc(count1)
	else if a[j] = cur2 then
   	  inc(count2)
	else begin
	  if a[j - 1] =	____②_____	then	//（3 分）
	  begin
	    while count2 > 0 do
		begin
		  if a[i] = cur1 then
		     dec(count1)
		  else
		     dec(count2);
		  inc(i);
	   end;
	   cur2 := a[j];
	   count2 := 1;
	end
	else begin
	while count1 > 0 do
	begin
	  if a[i] = cur1 then
	      ____③_____	//（2 分）
	  else
	      ____④_____	;	//（2 分）
	  inc(i);
	end;
	____⑤_____	;	//（3 分）
	count1 := 1;
  end;
end;
if (ans_length < j - i + 1) then
  begin
   ans_length := j - i + 1;
   ans_start := i;
   ans_end := j;
  end;
  end;
 for i := ans_start to ans_end do
    write(a[i], ' ');
end.

查看参考答案