2011年NOIP提高组初赛真题

一、单项选择题（共10题，每题1.5分，共15分，每题有且仅有一个正确选项。）

1. 1．在二进制下，1100011 +（ ）= 1110000。

• A. 1011
• B. 1101
• C. 1010
• D. 1111

2. 字符“A”的ASCII码为十六进制41，则字符“Z”的ASCII码为十六进制的（ ）。

• A. 66
• B. 5A
• C. 50
• D. 视具体的计算机而定

3. 右图是一棵二叉树，它的先序遍历是（ ）。

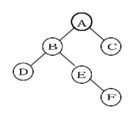
• A. ABDEFC
• B. DBEFAC
• C. DFEBCA
• D. ABCDEF

4. 寄存器是（ ）的重要组成部分。

• A. 硬盘
• B. 高速缓存
• C. 内存
• D. 中央处理器（CPU）

5. 广度优先搜索时，需要用到的数据结构是（ ）。

• A. 链表
• B. 队列
• C. 栈
• D. 散列表

6. 在使用高级语言编写程序时，一般提到的“空间复杂度”中的“空间”是指（ ）。

• A. 程序运行时理论上所占的内存空间
• B. 程序运行时理论上所占的数组空间
• C. 程序运行时理论上所占的硬盘空间
• D. 程序源文件理论上所占的硬盘空间

7. 应用快速排序的分治思想，可以实现一个求第K大数的程序。假定不考虑极端的最坏情况，理论上可以实现的最低的算法时间复杂度为（ ）。

• A. O(n2)
• B. O(n log n)
• C. O(n)
• D. O(1)

8. 为解决Web应用中的不兼容问题，保障信息的顺利流通，（ ）制定了一系列标准，涉及HTML、XML、CSS等，并建议开发者遵循。

• A. 微软
• B. 美国计算机协会（ACM）
• C. 联台国教科文组织
• D. 万维网联盟（W3C）

9. 体育课的铃声响了，同学们都陆续地奔向操场，按老师的要求从高到矮站成一排。每个同学按顺序来到操场时，都从排尾走向排头，找到第一个比自己高的同学，并站在他的后面。这种站队的方法类似于（ ）算法。

• A. 快速排序
• B. 插入排序
• C. 冒泡排序
• D. 归并排序

10. 1956年（ ）授予肖克利（William Shockley）、巴丁（John Bardeen）和布拉顿（Walter Brattain)，以表彰他们对半导体的研究和晶体管效应的发现。

• A. 诺贝尔物理学奖
• B. 约翰?冯?诺依曼奖
• C. 图灵奖
• D. 高德纳奖（Donald
• E. Knuth Prize）

二、不定项选择题（共10题，每题1.5分，共15分。每题有一个或多个正确选项。多选或少选均不得分。）

11. 如果根结点的深度记为1，则一棵恰有2011个叶子结点的二叉树的深度可能是（ ）。

• A. 10
• B. 11
• C. 12
• D. 2011

12. 在布尔逻辑中，逻辑“或”的性质有（ ）。

• A. 交换律：P V Q = Q V P
• B. 结台律：P V ( Q V R ) = ( P V Q ) V R
• C. 幂等律：P V P = P
• D. 有界律：P V 1 = 1 （1表示逻辑真）

13. 一个正整数在十六进制下有100位，则它在二进制下可能有（ ）位。

• A. 399
• B. 400
• C. 401
• D. 404

14. 汇编语言（ ）。

• A. 是一种与具体硬件无关的程序设计语言
• B. 在编写复杂程序时，相对于高级语言而言代码量较大，且不易调试
• C. 可以直接访问寄存器、内存单元、I/O端口
• D. 随着高级语言的诞生，如今已完全被淘汰，不再使用

15. 现有一段文言文，要通过二进制哈夫曼编码进行压缩。简单起见，假设这段文言文只由4个汉字“之”、“乎”、“者”、“也”组成，它们出现的次数分别为700、600、300、400。那么，“也”字的编码长度可能是（ ）。

• A. 1
• B. 2
• C. 3
• D. 4

16. 生物特征识别，是利用人体本身的生物特征进行身份认证的一种技术。目前，指纹识别、虹膜识别、人脸识别等技术己广泛应用于政府、银行、安全防卫等领域。以下属于生物特征识别技术及其应用的是（ ）。

• A. 指静脉验证
• B. 步态验证
• C. ATM机密码验证
• D. 声音验证

17. 对于序列“7、5、1、9、3、6、8、4”，在不改变顺序的情况下，去掉（ ）会使逆序对的个数减少3。

• A. 7
• B. 5
• C. 3
• D. 6

18. 计算机中的数值信息分为整数和实数（浮点数）。实数之所以能表示很大或者很小的数，是由于使用了（ ）。

• A. 阶码
• B. 补码
• C. 反码
• D. 较长的尾数

19. 对右图使用Dijkstra算法计算S点到其余各点的最短路径长度时，到B点的距离d[B]初始时赋为8，在算法的执行过程中还会出现的值有（ ）。

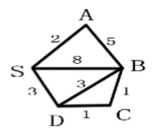
• A. 3
• B. 7
• C. 6
• D. 5

20. 为计算机网络中进行数据交换而建立的规则、标准或约定的集合成为网络协议。下列英文缩写中，（ ）是网络协议。

• A. HTTP
• B. TCP/IP
• C. FTP
• D. WWW

三、问题求解（共2题，每题5分，共计10分） 

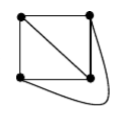
21. 平面图是可以画在平面上，且它的边仅在顶点上才能相交的简单无向图。4个顶点的平面图至多有6条边，如右图所示。那么，5个顶点的平面图至多有_________条边。

22. 定义一种字符串操作，一次可以将其中一个元素移到任意位置。举例说明，对于字符串“BCA”，可以将A移到B之前，变成字符串“ABC”。如果要将字符串“DACHEBGIF”变成“ABCDEFGHI”，最少需要_________次操作。

四、阅读程序写结果（共4题，每题8分，共计32分）

23.

const
	SIZE=100; 
var
	n,i,sum,x:integer;
	A:array[1..SIZE]of integer;
 
begin
	readln(n);
	fillchar(a,sizeof(a),0);
	for i:=1 to n do
	begin
	 read(x);
	 inc(a[x]);
	end;
	i:=0;
	sum:=0;
	while sum<(n div 2 + 1) do
	begin
	 inc(i);
	 sum:=sum+a[i];
	 end;
	 writeln(i);
end.
输入：
11
4 5 6 6 4 3 3 2 3 2 1
输出：____①_____

24.

var
	n:integer;
 
procedure f2(x,y:integer);
forward;
procedure f1(x,y:integer);
begin
	if x<n then
		f2(y,x+y);
	end;
 
	procedure f2(x,y:integer);
	begin
		write(x,’ ‘);
		f1(y,x+y);
	end;
 
	begin
		readln(n);
		f1(0,1);
	end.
输入：30
输出：____①_____

25.

const
	v = 100;
var
	visited:array[1..v]of boolean;
	e:array[1..v,1..v]of integer;
	n,m,ans,i,j,a,b,c:integer;
	
	procedure dfs(x,len:integer);
	var
		i:integer;
	begin
		visited[x] := true;
		if len > ans then
			ans:=len;
		for i:=1 to n do
			if (not visited(i)) and(e[x,i] <> -1) then
				dfs(I,len+e[x,i]);
		visited[x] := false;
	end;
 
	begin
		readln(n,m);
		for i:=1 to n do
			for j:=1 to n do
				e[i][j] := -1;
		for i:=1 to m do
		begin
			readln(a,b,c);
			e[a][b]:=c;
			e[b][a]:=c;
		end;
		for i:=1 to n do
			visited[i]:=false;
		ans:=0;
		for i:=1 to n do
			dfs(i,0);
		writeln(ans);
	end.
 
	输入：
	4 6
	1 2 10
	2 3 20
	3 4 30
	4 1 40
	1 3 50
	2 4 60
输出：____①_____

26.

const
	SIZE = 10000;
	LENGTH = 10;
var
	sum : longint;
	n,m,I,j : integer;
	a:array[1..SIZE , 1..LENGTH]of integer;
 
function h(u , v :integer):integer;
var
	ans,i : integer;
begin
	ans:=0;
	for i:=1 to n do
	if a[u][i] <> a[v][i] then
		inc(ans);
	h := ans;
end;
 
begin
	readln(n);
	fillchar(a,sizeof (a),0);
	m:=1;
	repeat
		i := 1;
		while (i <=n) and (a[m][i] =1 ) do
			inc(i);
		if i>n then
			break;
		a[m][i]:=1;
		for j:=i + 1 to n do
			a[m][j] := a[m-1][j];
	until false;
	sum := 0;
	for i := 1 to m do
		for j := 1 to m do
			sum := sum + h(i,j);
		writeln(sum);
end.
输入：7
输出：____①_____

五、完善程序（第一题，每空2分，第二题，每空3分，共计28分）

27. （大整数开方）输入一个正整数n（1<=n<10^100）,试用二分法计算它的平方根的整数部分。

const
	SIZE=200; 
type
	hugeint = record
		len : integer;
		num : array[1..SIZE] of integer;
	end;	//len表示大整数的位数；num[1]表示个位、num[2]表示十位，以此类推（这个注释不是我带鱼灰写的，是原试题带有的）
var
	s : string;
	i : integer;
	target, left, middle, right : hugeint; 
function times(a, b : hugeint) : hugeint;
var
	i, j : integer;
	ans : hugeint;
begin
	fillchar(ans,sizeof(ans),0);
	for i:=1 to a.len do
		for j:=1 to b.len do
    ____①_____ :=ans.num[i + j - 1] + a.num[i] * b.num[j];
	for i:=1 to a.len+b.len do
	begin
		ans.num[i + 1] := ans.num[i + 1] + ans.num[i] div 10;
		____②_____	;	
		if ans.num[a.len + b.len] > 0
			then ans.len := a.len + b.len
			else ans.len := a.len + b.len - 1;
	end;
	times := ans;
end;
 
function add(a,b : hugeint) : hugeint;
	var
		i : integer;
		ans: hugeint;
begin
	fillchar(ans.num,sizeof(ans.num),0);
	if a.len>b.len
		then ans.len := a.len
		else ans.len := b.len;
	for i := 1 to ans.len do
	begin
		ans.num[i]:= ____③_____ ；
		ans.num[i+1] := ans.num[i+1] + ans.num[i] div 10;
		ans.num[i] := ans.num[i] mod 10;
	end;
	if ans.num[ans.len + 1]>0
		then inc(ans.len);
	add := ans;
end;
 
function average(a,b: hugeint) : hugeint;
var
	i : integer;
	ans : hugeint;
begin
	ans := add(a,b);
	for i:= ans.len downto 2 do
	begin
		ans.num[i-1] := ans.num[i-1] + ( ____④_____ ) *10;
		ans.num[i]:=ans.num[i] div 2;
	end;
	ans.num[1]:=ans.num[1] div 2;
	if ans.num[ans.len] = 0
		then dec(ans.len);
	average := ans;
end;
 
function plustwo(a : hugeint) : hugeint;
var
	i : integer;
	ans : hugeint;
begin
	ans := a;
	ans.num[1] := ans.num[1] + 2;
	i:=1;
	while (i <= ans.len) and (ans.num[i] >= 10) do
	begin
		ans.num[i + 1] := ans.num[i + 1] + ans.num[i] div 10;
		ans.num[i] := ans.num[i] mod 10;
		inc(i);
	end;
	if ans.num[ans.len + 1] > 0
		then ____⑤_____ ；
	plustwo := ans;
end;
 
function over(a , b: hugeint) : boolean;
var
	i: integer;
begin
	if ( ____⑥_____ ) then
	begin
		over := false;
		exit;
	end;
	if a.len > b.len then
	begin
		over := true;
		exit;
	end;
	for i := a.len downto 1 do
	begin
		if a.num[i] < b.num[i] then
		begin
			over := false;
			exit;
		end;
		if a.num[i] > b.num[i] then
		begin
			over := true;
			exit;
		end;
	end;
	over := false;
end;
 
begin
	readln(s);
	fillchar(target.num,sizeof(target.num),0);
	target.len := length(s);
	for i := 1 to target.len do
		target.num[i] := ord(s[target.len - i +1]) - ____⑦_____ ;
	fillchar(left.num,sizeof(left,num),0);
	left.len:=1;
	left.num[1]:=1;
	right:=target;
	repeat
		middle:=average(left,right);
		if over( ____⑧_____ )
			then right := middle
			else left := middle;
	until over(plustwo(left),right);
	for i:= left.len downto 1 do
		write(left.num[i]);
	writeln;
end.

28. （笛卡尔树）对于一个给定的两两不等的正整数序列，笛卡尔树是这样的一棵二叉树：首先，它是一个最小堆，即除了根结点外，每个结点的权值都大于父结点的权值；其次，它的中序遍历恰好就是给定的序列。例如，对于序列7、2、12、1、10、5、15、3，下图就是一棵树对应的笛卡尔树。现输入序列的规模n（1<=n<100）和序列的n个元素，试求其对应的笛卡尔树的深度d（根节点深度为1），以及有多少个叶节点的深度为d。

const
	SIZE = 100;
	INFINITY = 1000000;
 
var
	n , maxDeep, num , i : integer;
	a : array[1..SIZE] of integer;
 
procedure solve(left , right , deep : integer);
var
	i,j,min: integer;
begin
	if deep>maxDeep then
	begin
		maxDeep :=deep;
		num := 1;
	end
	else if deep=maxDeep then
	____①_____	;
	
	min := INFINITY;
	for i := left to right do
		if min > a[i] then
		begin
			min := a[i];
			____②_____ ;
		end;
	if left < j then
		____③_____ ;
	if j<right then
	____④_____;
end;
 
begin
	readln(n);
	for i := 1 to n do
		read(a[i]);
	maxDeep:=0;
	solve( 1, n, 1);
	writeln(maxDeep, ‘ ‘, num);
end.