2015年NOIP提高组初赛真题

一、单项选择题（共15 题，每题1.5 分，共计22.5 分；每题有且仅有一个正确选项）

1. 在计算机内部用来传送、存贮、加工处理的数据或指令都是以（）形式进行的。

A. 二进制码
B. 八进制码
C. 十进制码
D. 智能拼音码

2. 下列说法正确的是（）。

A. CPU 的主要任务是执行数据运算和程序控制
B. 存储器具有记忆能力，其中信息任何时候都不会丢失
C. 两个显示器屏幕尺寸相同，则它们的分辨率必定相同
D. 个人用户只能使用Wifi 的方式连接到Internet

3. 与二进制小数0.1 相等的十六进制数是（）。

A. 0.8
B. 0.4
C. 0.2
D. 0.1

4. 下面有四个数据组，每个组各有三个数据，其中第一个数据为八进制数，第二个数据为十进制数，第三个数据为十六进制数。这四个数据组中三个数据相同的是（）。

A. 120 82 50
B. 144 100 68
C. 300 200 C8
D. 1762 1010 3F2

5. 线性表若采用链表存储结构，要求内存中可用存储单元地址（）。

A. 必须连续
B. 部分地址必须连续
C. 一定不连续
D. 连续不连续均可

6. 今有一空栈S，对下列待进栈的数据元素序列a,b,c,d,e,f 依次进行进栈，进栈，出栈，进栈，进栈，出栈的操作，则此操作完成后，栈S 的栈顶元素为（）。

A. f
B. c
C. a
D. b

7. 前序遍历序列与后序遍历序列相同的二叉树为（）。

A. 非叶子结点只有左子树的二叉树
B. 只有根结点的二叉树
C. 根结点无右子树的二叉树
D. 非叶子结点只有右子树的二叉树

8. 如果根的高度为1，具有61 个结点的完全二叉树的高度为（）。

A. 5
B. 6
C. 7
D. 8

9. 6 个顶点的连通图的最小生成树，其边数为（）。

A. 6
B. 5
C. 7
D. 4

10. 设某算法的计算时间表示为递推关系式T(n) = T(n - 1) + n（n 为正整数）及T(0) = 1，则该算法的时间复杂度为（）。

A. O(log n)
B. O(n log n)
C. O(n)
D. O(n2)

11. 具有n 个顶点，e 条边的图采用邻接表存储结构，进行深度优先遍历和广度优先遍历运算的时间复杂度均为（）。

A. Θ(n2)
B. Θ(e2)
C. Θ(ne)
D. Θ(n + e)

12. 在数据压缩编码的应用中，哈夫曼（Huffman）算法是一种采用了（）思想的算法。

A. 贪心
B. 分治
C. 递推
D. 回溯

13. 双向链表中有两个指针域，llink和rlink，分别指回前驱及后继，设p指向链表中的一个结 点，q指向一待插入结点，现要求在p前插入q，则正确的插入为（）。

A. p->llink = q; q->rlink = p; p->llink->rlink = q; q->llink = p->llink;
B. q->llink = p->llink; p->llink->rlink = q; q->rlink = p; p->llink = q->rlink;
C. q->rlink = p; p->rlink = q; p->llink->rlink = q; q->rlink = p;
D. p->llink->rlink = q; q->rlink = p; q->llink

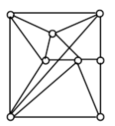14. 对图G 中各个结点分别指定一种颜色，使相邻结点颜色不同，则称为图G 的一个正常着色。正常着色图G 所必需的最少颜色数，称为G 的色数。那么下图的色数是（）

A. 3
B. 4
C. 5
D. 6

15. 在NOI 系列赛事中参赛选手必须使用由承办单位统一提供的设备。下列物品中不允许选手自带的是（）。

A. 鼠标
B. 笔
C. 身份证
D. 准考证

二、不定项选择题（共5 题，每题1.5 分，共计7.5 分；每题有一个或多个正确选项，多选或少选均不得分）

16. 以下属于操作系统的有（）。

A. Windows XP
B. UNIX
C. Linux
D. Mac OS

17. 下列属于视频文件格式的有（）。

A. AVI
B. MPEG
C. WMV
D. JPEG

18. 下列选项不是正确的IP 地址的有（）。

A. 202.300.12.4
B. 192.168.0.3
C. 100:128:35:91
D. 111-103-35-21

19. 下列有关树的叙述中，叙述正确的有（）。

A. 在含有n 个结点的树中，边数只能是(n-1)条
B. 在哈夫曼树中，叶结点的个数比非叶结点个数多1
C. 完全二叉树一定是满二叉树
D. 在二叉树的前序序列中，若结点u 在结点v 之前，则u一定是v的祖先

20. 以下图中一定可以进行黑白染色的有（）。（黑白染色：为各个结点分别指定黑白两种颜色之一，使相邻结点颜色不同。）

A. 二分图
B. 完全图
C. 树
D. 连通图

三、问题求解（共2 题，每题5 分，共计10 分；每题全部答对得5 分，没有部分分）

21. 在1 和2015 之间（包括1 和2015 在内）不能被4 、5、6 三个数任意一个数整除的数有_________个。

22. 结点数为5 的不同形态的二叉树一共有_________种。（结点数为2 的二叉树一共有2种：一种是根结点和左儿子，另一种是根结点和右儿子。）

四、阅读程序写结果（共4 题，每题8 分，共计32 分）

23.

#include <iostream>
using namespace std;
struct point {
    int x;
    int y;
};
int main() {
    struct EX{
         int a;
         int b;
         point c;
    } e; 
   e.a = 1; 
   e.b = 2; 
   e.c.x = e.a + e.b;
   e.c.y = e.a * e.b; 
   cout << e.c.x << ',' << e.c.y << endl;
    return 0;
} 
输出：____①_____

24.

#include <iostream> 
using namespace std; 
void fun(char *a, char *b) {
    a = b;
    (*a)++;
} 
int main() { 
   char c1, c2, *p1, *p2;
    c1 = 'A';
    c2 = 'a';
    p1 = &c1;
    p2 = &c2;
    fun(p1, p2); 
   cout << c1 << c2 << endl;
    return 0;
} 
输出：____①_____

25.

#include <iostream> 
#include <string>
using namespace std;
int main() { 
   int len, maxlen;
    string s, ss;
    maxlen = 0;
    do { 
       cin >> ss; 
       len = ss.length();
        if (ss[0] == '# ')
            break; 
       if (len > maxlen) {
            s = ss; 
           maxlen = len;
        } 
   } while (true);
    cout << s << endl;
    return 0;
}
输入：
I
am
a
citizen     
of     
China
#
输出：____①_____

26.

#include <iostream> 
using namespace std; 
int fun(int n, int fromPos, int toPos) {
     int t, tot;
     if (n == 0)
         return 0; 
    for (t = 1; t <= 3; t++) 
        if (t != fromPos && t != toPos)
             break;
     tot = 0; 
    tot += fun(n - 1, fromPos, t);
     tot++; 
    tot += fun(n - 1, t, toPos);
     return tot;
 } 
int main() {
     int n;
     cin >> n; 
    cout << fun(n, 1, 3) << endl;
     return 0;
 }
输入：5
输出：____①_____

五、完善程序（共2 题，每题14 分，共计28 分）

27. （双子序列最大和）给定一个长度为n（3 ≤ n ≤ 1000 ）的整数序列，要求从中选出两个连续子序列，使得这两个连续子序列的序列和之和最大，最终只需输出这个最大和。一个连续子序列的序列和为该连续子序列中所有数之和。要求：每个连续子序列长度至少为1，且两个连续子序列之间至少间隔1 个数。（第五空4分，其余2.5分）


#include <iostream>
using namespace std;
const int MAXN = 1000;
int n, i, ans, sum;
int x[MAXN];
int lmax[MAXN]; 
// lmax[i]为仅含x[i]及x[i]左侧整数的连续子序列的序列和中，最大的序列和
int rmax[MAXN]; 
// rmax[i]为仅含x[i]及x[i]右侧整数的连续子序列的序列和中，最大的序列和
int main() {
    cin >> n; 
   for (i = 0; i < n; i++)
        cin >> x[i]; 
   lmax[0] = x[0]; 
   for (i = 1; i < n; i++)
        if (lmax[i - 1] <= 0)
            lmax[i] = x[i];
        else 
           lmax[i] = lmax[i - 1] + x[i];
    for (i = 1; i < n; i++) 
       if (lmax[i] < lmax[i - 1])
            lmax[i] = lmax[i - 1];
        ____①_____   ; 
   for (i = n - 2; i >= 0; i--)
        if (rmax[i + 1] <= 0)
            ____②_____   ;    
        else 
            ____③_____   ;            
   for (i = n - 2; i >= 0; i--)
        if (rmax[i] < rmax[i + 1])
             ____④_____   ;   
   ans = x[0] + x[2]; 
   for (i = 1; i < n - 1; i++) {
        sum = ____⑤_____   ;      
      if (sum > ans)
            ans = sum;
    } 
   cout << ans << endl;
    return 0;
}

28. （最短路径问题）无向连通图G 有n 个结点，依次编号为0,1,2,...,(n-1)。用邻接矩阵的形式给出每条边的边长，要求输出以结点0 为起点出发，到各结点的最短路径长度。 使用Dijkstra 算法解决该问题：利用dist 数组记录当前各结点与起点的已找到的最短路径长度；每次从未扩展的结点中选取dist 值最小的结点v 进行扩展，更新与v 相邻的结点的dist 值；不断进行上述操作直至所有结点均被扩展，此时dist 数据中记录的值即为各结点与起点的最短路径长度。（第五空2 分，其余3 分）

 
#include <iostream>
 using namespace std;
 const int MAXV = 100;
 int n, i, j, v; 
int w[MAXV][MAXV];
//邻接矩阵，记录边长 
// 其中w[i][j]为连接结点i 和结点j 的无向边长度，若无边则为-1
int dist[MAXV]; 
int used[MAXV];
//记录结点是否已扩展（0：未扩展；1：已扩展） 
int main() {
     cin >> n; 
    for (i = 0; i < n; i++)
         for (j = 0; j < n; j++)
             cin >> w[i][j];
     dist[0] = 0; 
    for (i = 1; i < n; i++)
         dist[i] = -1; 
    for (i = 0; i < n; i++)
         used[i] = 0;
     while (true) {
            ____①_____ ;    
        for (i = 0; i < n; i++)
            if (used[i] != 1 && dist[i] != -1 && (v == -1 || ____②_____ )) 
              ____③_____ ; 
            if (v == -1)
             break;
              ____④_____ ;    
        for (i = 0; i < n; i++)
            if (w[v][i] != -1 && (dist[i] == -1 || ____⑤_____ ))
                 dist[i] = dist[v] + w[v][i];
     } 
    for (i = 0; i < n; i++) 
        cout << dist[i] << endl;
     return 0;
 }

查看参考答案