2012年NOIP提高组初赛真题
- 一、单项选择题(共10题,每题1.5分,共计15分;每题有且仅有一个正确选项)
-
- 1. 目前计算机芯片(集成电路)制造的主要原料是( ),它是一种可以在沙子中提炼出的物质。
-
- A. 硅
- B. 铜
- C. 锗
- D. 铝
-
- 2. ( )是主要用于显示网页服务器或者文件系统的HTML文件的内容,并让用户与这些文件交互的一种软件。
-
- A. 资源管理器
- B. 浏览器
- C. 电子邮件
- D. 编译器
-
- 3. 目前个人电脑的( )市场占有率最靠前的厂商包括Intel、AMD等公司。
-
- A. 显示器
- B. CPU
- C. 内存
- D. 鼠标
-
- 4. 无论是TCP/IP模型还是OSI模型,都可以视为网络的分层模型,每个网络协议都会被归入某一层中。如果用现实生活中的例子来比喻这些“层”,以下最恰当的是( )。
-
- A. 中国公司的经理与波兰公司的经理交互商业文件
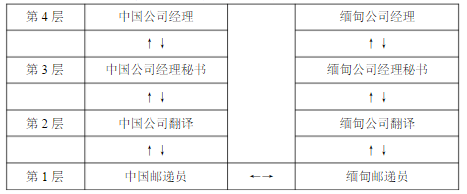
- B. 军队发布命令

- C. 国际会议中,每个人都与他国地位对等的人直接进行会谈
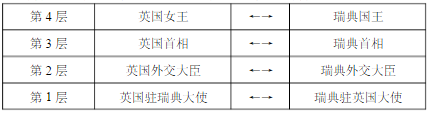
- D. 体育比赛中,每一级比赛的优胜者晋级上一级比赛
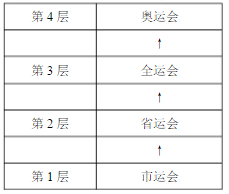
- A. 中国公司的经理与波兰公司的经理交互商业文件
-
- 5. 如里不在快速排序中引入随机化,有可能导致的后果是( )。
-
- A. 数组访问越界
- B. 陷入死循环
- C. 排序结果错误
- D. 排序时间退化为平方级
-
- 6. 1946年诞生于美国宾夕法尼亚大学的ENIAC属于( )计算机。
-
- A. 电子管
- B. 晶体管
- C. 集成电路
- D. 超大规模集成电路
-
- 7. 在程序运行过程中,如果递归调用的层数过多,会因为( )引发错误。
-
- A. 系统分配的栈空间溢出
- B. 系统分配的堆空间溢出
- C. 系统分配的队列空间溢出
- D. 系统分配的链表空间溢出
-
- 8. 地址总线的位数决定了CPU可直接寻址的内存空间大小,例如地址总线为16位,其最大的可寻址空间为64KB。如果地址总线是32位,则理论上最大可寻址的内存空间为( )。
-
- A. 128KB
- B. 1MB
- C. 1GB
- D. 4GB
-
- 9. 以下不属于3G(第三代移动通信技术)标准的是( )。
-
- A. GSM
- B. TD-SCDMA
- C. CDMA2000
- D. WCDMA
-
- 10. 仿生学的问世开辟了独特的科学技术发展道路。人们研究生物体的结构、功能和工作原理,并将这些原理移植于新兴的工程技术中。以下关于仿生学的叙述,错误的是( )
-
- A. 由研究蝙蝠,发明雷达
- B. 由研究蜘蛛网,发明因特网
- C. 由研究海豚,发明声纳
- D. 由研究电鱼,发明伏特电池
- 二、不定项选择题(共10题,每题1.5分,共计15分;每题有一个或多个正确选项,多选或少选均不得分)
-
- 11. 如果对于所有规模为n的输入,一个算法均恰好进行( )次运算,我们可以说该算法的时间复杂度为O(2^n)。
-
- A. 2^(n+1)+
- B. 3^n
- C. n*2^n
- D. 2^2n
-
- 12. 从顶点0A 出发,对有向图( )进行广度优先搜索(BFS)时,一种可能的遍历顺序是A0,A1,A2,A3,A4。
-
- A.
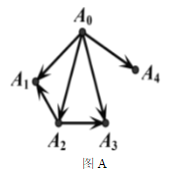
- B.
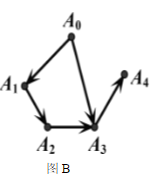
- C.
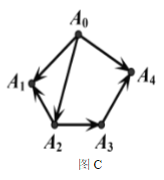
- D.

- A.
-
- 13. 如果一个栈初始时为空,且当前栈中的元素从栈顶到栈底依次为a,b,c(如右图所示),另有元素d已经出栈,则可能的入栈顺序是( )。
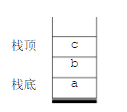
-
- A. a, b, c, d
- B. b, a, c, d
- C. a, c, b, d
- D. d, a, b, c
- 13. 如果一个栈初始时为空,且当前栈中的元素从栈顶到栈底依次为a,b,c(如右图所示),另有元素d已经出栈,则可能的入栈顺序是( )。
-
- 14. 在计算机显示器所使用的RGB颜色模型中,( )属于三原色之一。
-
- A. 黄色
- B. 蓝色
- C. 紫色
- D. 绿色
-
- 15. 一棵二叉树一共有19个节点,其叶子节点可能有( )个。
-
- A. 1
- B. 9
- C. 10
- D. 15
-
- 16. 已知带权有向图G上的所有权值均为正整数,记顶点u到顶点v的最短路径的权值为d(u,v)。若v1v2v3v4v5 是图G上的顶点,且它们之间两两都存路径可达,则以下说法正确的有( )。
-
- A. V1 到v2的最短路径可能包含一个环
- B. D(v1,v2)=d(v2,v1)
- C. D(v1,v3)<=d(v1,v2)+d(v2,v3)
- D. 如果v1->v2->v3->v4->v5是v1到v5的一条最短路径那么v2->v3->v4是v2到v4的最短路径
-
- 17. 逻辑异或(⊕)是一种二元运算,其真值表如下所示。
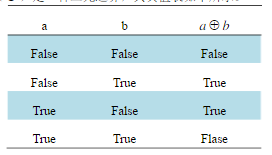
以下关于逻辑异或的性质,正确的有( )。 -
- A. 交换律:a ⊕ b = b ⊕ a
- B. 结合律:(a ⊕ b) ⊕ c = a ⊕ (b ⊕ c)
- C. 关于逻辑与的分配律:a ⊕ (b ∧ c) = (a ⊕ b) ∧ (a ⊕ c)
- D. 关于逻辑或的分配律:a ⊕ (b ∨ c) = (a ⊕ b) ∨ (a ⊕ c)
- 17. 逻辑异或(⊕)是一种二元运算,其真值表如下所示。
-
- 18. 十进制下的无限循环小数(不包括循环节内的数字均为0成均为9的平凡情况),在二进制下有可能是( )。
-
- A. 无限循环小数(不包括循环节内的数字均为0或均为9)
- B. 无限不循环小数
- C. 有限小数
- D. 整数
-
- 19. ( )是目前互联网上常用的E-mail服务协议。
-
- A. HTTP
- B. FTP
- C. POP3
- D. SMTP
-
- 20. 以下关于计算复杂度的说法中,正确的有( )。
-
- A. 如果一个问题不存在多项式时间的算法,那它一定是NP类问题
- B. 如果一个问题不存在多项式时间的算法,那它一定不是P类问题
- C. 如果一个问题不存在多项式空间的算法,那它一定是NP类问题
- D. 如果一个问题不存在多项式空间的算法,那它一定不是P类问题
- 三、问题求解(共2题,每题5分,共计10分)
-
- 21. 本题中,我们约定布尔表达式只能包含p, q, r三个布尔变量,以及“与”(∧)、“或”
(∨)、“非”(¬)三种布尔运算。如果无论p, q, r如何取值,两个布尔表达式的值总是相同,则称它们等价。例如,(p∨q)∨r和p∨(q∨r)等价,p∨¬p和q∨¬q也等价;而p∨q和p∧q不等价。那么,两两不等价的布尔表达式最多有_________个。
- 21. 本题中,我们约定布尔表达式只能包含p, q, r三个布尔变量,以及“与”(∧)、“或”
-
- 22.
 对于一棵二叉树,独立集是指两两互不相邻的节点构成的集合。例如,图1有5个不同的独立集(1个双点集合,3个单点集合、1个空集),图2有14个不同的独立集。那么图3有_________个不同的独立集。
对于一棵二叉树,独立集是指两两互不相邻的节点构成的集合。例如,图1有5个不同的独立集(1个双点集合,3个单点集合、1个空集),图2有14个不同的独立集。那么图3有_________个不同的独立集。
- 22.
- 四、阅读程序写结果。(共4题,每题8分,共计32分)
-
- 23.
-
var n,i,temp,sum:integer; a :array[1..100] of integer; begin readln(n); for i:=1 to n do read(a[i]); for i:=1 to n-1 do if a[i]>a[i+1] then begin temp := a[i]; a[i] := a[i+1]; a[i+1] := temp; end; for i:=n downto 2 do if a[i]<a[i-1] then begin temp := a[i]; a[i] := a[i-1]; a[i-1] := temp; end; sum := 0; for i:=2 to n-1 do inc(sum,a[i]); writeln(sum div (n-2)); end. 输入: 8 40 70 50 70 20 40 10 30 输出:____①_____
-
- 24.
-
var n,i,ans:integer; function gcd(a,b :integer) : integer; begin if a mod b=0 then gcd :=0; else gcd := gcd(b,a mod b); end; begin readln(n); ans := 0; for i:=1 to n do if gcd(n,i)=i then ans := ans + 1; writeln(ans); end. 输入:120 输出:____①_____
-
- 25.
-
var data : array[1..20] of integer; n,i,h,ans: integer; procedure merge; begin data[h-1] := data[h-1] + data[h]; dec(h); inc(ans); end; begin readln(n); h := 1; data[h] := 1; ans := 0; for i:=2 to n do begin inc(h); data[h] := 1; while (h>1) and (data[h]=data[h-1]) do merge; end; writeln(ans); end. (1) 输入:8 (2) 输入:2012 输出:____①_____
-
- 26.
-
var left, right, father:array[1..20] of integer; sl, s2, s3:string; n,ana :integer; procedure check(x:integer); begin if left[x]>0 then check(left[x)); s3 := s3 + sl[x]; if right[x]>0 then check(right[x]); end; procedure calc(x,dep :integer); begin ans:= ans + dep*(ord(sl[x])-ord('A')+1); if left[x] > 0 then calc(left[x],dep+l); if right[x]> 0 then calc(right[x),dep+l); end; procedure dfs(x,th :integer); begin if th = n+1 then begin s3 :=''; check(1); if s2=s3 then begin ans := 0; calc(1,1); writeln(ans); end; exit; end; if (left[x]=0) and (right[x]=0) then begin left[x) := th; father[th] := x; dfs(th, th+1); father[th] := 0; left[x] := 0; end; if right[x] = 0 then begin right[x] := th; father[th] := X; dfs(th, th+1); father[th] := 0; right[x] := 0; end; if (father[x] > 0) then dfs(father[x],th); end; begin readln(s1); readln(s2); n := length(s1); fillchar(left,sizeof(left),0); fillchar(right,sizeof(right),0); fillcahr(father,sizeof(father),0); dfs(1,2); end. 输入: ABCDEF BCAEDF 输出:____①_____
- 五、完善程序(第1题第2空3分,其余每空2.5分,共计28分)
-
- 27. (排列数)输入两个正整数 ,在 中任取 个数,按字典序从小到大输出所有这样的排列。例如
输入:3 2
输出:1 2
1 3
2 1
2 3
3 1
3 2 -
const SIZE=20; var used:array [1..SIZE] of boolean; data:array [1..SIZE] of integer; n,m,i,j,k:integer; flag:boolean; begin readln(n,m); fillchar(used,sizeof(used),false); for i:=1 to m do begin data[i] := i; used[i] := true; end; flag := true; while flag do begin for i:=1 to m-1 do write(data[i],' '); writeln(data[m]); flag := ____①_____ ; for i := m downto 1 do begin ____②_____ ; for j := data[i]+1 to n do if used[j] = false then begin used[j] := true; data[i] := ____③_____ ; flag := true; break; end; if flag then begin for k:= i+l to m do for j:= 1 to ____④_____ do if used[j]=false then begin data[k] := j; used[j] := true; break; end; ____⑤_____ ; end; end; end; end.
- 27. (排列数)输入两个正整数 ,在 中任取 个数,按字典序从小到大输出所有这样的排列。例如
-
- 28. (新壳栈)小Z设计了一种新的数据结构“新壳栈”。首先,它和传统的栈一样支持压入、弹出操作。此外,其栈顶的前c个元素是它的壳,支持翻转操作。其中,c>2是一个固定的正整数,表示壳的厚度。小Z还希望,每次操作,无论是压入、弹出还是翻转,都仅用与c无关的常数时间完成。聪明的你能帮助她编程实现“新壳栈”吗?
程序期望的实现效果如以下两表所示。其中,输入的第一行是正整数c,之后每行输入都是一条指令。另外,如遇弹出操作时栈为空,或翻转操作时栈中元素不足c个,应当输出相应的错误信息。 -
const NSIZE = 100000; CSIZE = 1000; var n,c,r,tail,head :longint; s : array[1..NSIZE] of longint; //数组s模拟一个栈,n为栈的元素个数 q :array[1..CSIZE] of longint; //数组q模拟一个循环队列,tail为队尾的下标,head为队头的下标 direction,empty :boolean; function previous(k :longint) :longint; begin if direction then previous := ((k+c-2) mod c) + 1; else previous := (k mod c) + 1; end; function next(k :longint) :longint; begin if direction then ____①_____ else next := ((k+c-2) mod c)+1; end; procedure push; var element :longint; begin read(element); if next(head) = tail then begin inc(n); ____②_____ ; tail := next(tail); end; if empty then empty := false else head := next(head); ____③_____ := element; end; procedure pop; begin if empty then begin writeln('Error: the stack is empty!'); exit; end: writeln( ____④_____ ); if tail = head then empty := true else begin head := previous(head); if n > 0 then begin tail := previous(tail); ____⑤_____ := s[n]; dec(n); end; end; end; procedure reverse; var temp :longint; begin if ____⑥_____ = tail then begin direction := not direction; temp := head; head := tail; tail := temp; end else writeln('Error:less than',c,' elements in the stack!'); end; begin readln(c); n := 0; tail := 1; head := 1; empty := true; direction := true; repeat read(r); case r of 1: push; 2: pop; 3: reverse; end; until r = 0; end.
- 28. (新壳栈)小Z设计了一种新的数据结构“新壳栈”。首先,它和传统的栈一样支持压入、弹出操作。此外,其栈顶的前c个元素是它的壳,支持翻转操作。其中,c>2是一个固定的正整数,表示壳的厚度。小Z还希望,每次操作,无论是压入、弹出还是翻转,都仅用与c无关的常数时间完成。聪明的你能帮助她编程实现“新壳栈”吗?