喵了个喵(meow)

小 E 喜欢上了一款叫做《喵了个喵》的游戏。这个游戏有一个牌堆和 $n$ 个可以从栈底删除元素的栈，任务是要通过游戏规则将所有的卡牌消去。开始时牌堆中有 $m$ 张卡牌，从上到下的图案分别是 $a_1$, $a_2$, · · · , $a_m$。所有的卡牌一共有 $k$ 种图案，从 $1$ 到$ k$编号。牌堆中每一种图案的卡牌都有偶数张。开始时所有的栈都是空的。这个游戏有两种操作：
• 选择一个栈，将牌堆顶上的卡牌放入栈的顶部。如果这么操作后，这个栈最上方的两张牌有相同的图案，则会自动将这两张牌消去。
• 选择两个不同的栈，如果这两个栈栈底的卡牌有相同的图案，则可以将这两张牌消去，原来在栈底上方的卡牌会成为新的栈底。如果不同，则什么也不会做。
这个游戏一共有 $T$ 关，小 E 一直无法通关。请你帮小 E 设计一下游戏方案，即对于游戏的每一关，给出相应的操作序列使得小 E 可以把所有的卡牌消去。

第一行包含一个正整数 $T$，表示数据组数。
接下来一共 $T$ 组数据，在每组数据中：
第一行包含三个正整数 $n$, $m$, $k$，分别表示栈的个数、卡牌的个数、卡牌上图案的种类。
第二行包含 $m$ 个正整数，分别表示 $a_1$, $a_2$, · · · , $a_m$，分别从上到下表示牌堆中卡牌的图案。
输入数据保证有解。

对于每一组数据，输出若干行。
其中第一行包含一个正整数 $op$，表示操作的次数。你需要保证 $m ≤ op ≤ 2 × m$。
接下来 $op$ 行，每行包含两个或三个正整数，整数之间用一个空格隔开。
若为两个整数 $1\  s$，则进行一次第一个操作并选择栈 s。
若为三个整数 $2\  s_1\  s_2$，则进行一次第二个操作并选择栈 $s_1$ 和 $s_2$。
你需要保证 $1 ≤ s, s_1, s_2 ≤ n$，且 $s_1≠ s_2$。

1
2 4 2
1 2 1 2

5
1 1
1 1
1 2
2 1 2
1 1

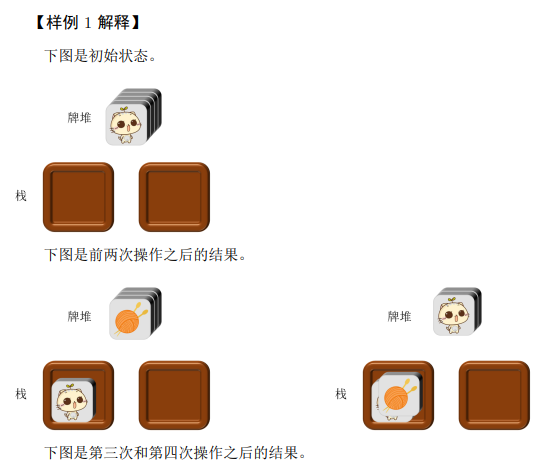
【数据范围】
设 $S$ 为所有 $T$ 组数据中 $m$ 的总和。
对于所有数据，保证 $S ≤ 2 × 10^6$，$1 ≤ n ≤ 300$，$1 ≤ a_i ≤ k$。

测试点	T =	n	k =	m ≤
1 ∼ 3	1001	≤ 300	2n − 2	无限制
4 ∼ 6	1002	= 2	2n-1
7 ∼ 10	3	= 3		14
11 ∼ 14	1004			无限制
15 ∼ 20	1005	≤ 300

【评分方式】
对于每一组数据，若在按顺序进行所有操作后，牌堆为空且所有的栈均为空，则认为你的答案正确。
【提示】
你可以通过 T 的个位数来判断这个测试点是属于哪一类数据。
你的输出不需要与样例输出一致，输出任意一个合法解即可得分。